Any Real Number Can Be Written as a Continued Fraction

Real numbers can be represented by decimals or by continued fractions, but both of these systems have the problem that the representations are not unique. This nonuniqueness can introduce ugly complications into proofs that use these representations, in particular those regarding the cardinality of $\mathbb R$.

In this post I'll explain what causes these complications, and then define a system that avoids them. In particular I'll define an elegant and order-preserving bijection from the interval $[0,1)$ to the set $\mathbb N \to\mathbb N$ of sequences of natural numbers.

(In case this notation is unfamiliar to readers, the set $[x,y)$ contains all the real numbers from $x$ to $y$, including $x$ but not including $y$. The set $A\to B$ contains all functions from $A$ to $B$. Also, I use the convention that $\mathbb N$ contains $0$.)

Cantor's problem

Real numbers don't have unique decimal representations. Every number of the form $n/10^m$ has one expansion which is eventually $0$s and one expansion which is eventually $9$s.

\begin{gather} 0.73482000000\dots\\ =\\ 0.73481999999\dots \end{gather}

This fact caused a problem for Cantor in his work on cardinality.

In 1877 Cantor was trying to find a bijection between the unit square and the unit interval, and wrote to Dedekind suggesting the function that simply interleaves digits.

\begin{align*} [0,1)^2&\to[0,1)\\ (0.x_0x_1x_2\dots,0.y_0y_1y_2\dots)&\mapsto 0.x_0y_0x_1y_1x_2y_2\dots \end{align*}

This seems like it should be a bijection, since you can recover the two inputs by taking every-other digit of the output.

But Dedekind was quick to point out that this construction doesn't quite work. The function isn't well defined because some numbers have more than one decimal representation. For example $0.1 = 0.0\overline{9}$, and so $(0.1,0.2)$ might be sent to $0.12$ or to $0.02\overline{90}$.

You can force the function to be well defined by picking just one of these representations. But then it stops being a bijection. For example if $(0.1, 0.2)$ gets sent to $0.12$, then there's nothing that gets sent to $0.02\overline{90}$.

Cantor's second attempt

Cantor's next idea was to use continued fractions instead of decimal expansions. But this didn't work either.

(A quick introduction to Continued Fractions)

The continued fraction of a number is calculated by splitting it into its integer and fractional parts.

$$\pi=3 + 0.14159265\dots$$

One then takes the reciprocal of the fractional part and repeats the process.

$$\frac{1}{0.14159265\dots} = 7.0625133\dots = 7 + 0.0625133\dots$$

Continuing in this way one builds up a gigantic fraction of fractions

$$\pi=3+\cfrac{1}{7+\cfrac{1}{15+\cfrac{1}{1+\cfrac{1}{\ddots}}}}$$

which we write more compactly as $[3;7,15,1,\dots]$. This sequence of integers is the continued fraction representation of the number.

Because of the way they're defined, each term in the expansion except for the first is guaranteed to be greater than or equal to $1$. The leading term can take any value including negatives. For example $-7.5$ would be written as $-8+\frac{1}{2} = [-8;2]$. This is why the notation distinguishes the leading term by a semicolon.

If the original number was rational then the process is guaranteed to terminate by reaching some number with fractional part $0$. Conversely, the continued fraction of any irrational number is an infinite sequence.

The sizes of two numbers can be compared using their continued fractions. To see which of two numbers is larger one simply finds the first place at which their expansions differ and then checks which has the larger number at this position. However, the ordering at the odd-numbered positions is reversed. So for example $[1;1,3,\dots]$ is greater than $[1;1,2,\dots]$, but $[1;1,1,3,\dots]$ is less than $[1;1,1,2,\dots]$. (If one of the continued fractions is finite and agrees with the other for all its terms then the order is determined by how many terms it has. It's smaller if it has an even number of terms and larger otherwise.)

Other properties can also be determined from the continued fraction expansion. For example the numbers with expansions which are eventually periodic are precisely the quadratic irrationals.

So what was Cantor's second attempt? He discarded decimal expansions and instead tried interleaving the continued fractions.

$$([0;n_0,n_1,n_2\dots],[0;m_0,m_1,m_2\dots])\mapsto [0;n_0,m_0,n_1,m_1,n_2,m_2\dots]$$

Can you see why this also doesn't work? It's because the continued fractions of rational numbers have finite length.

With decimal expansions, a terminating expansion like $0.5$ is really a way of writing an infinite expansion which is eventually $0$s, in this case $0.5\overline{0}$. But with continued fractions the sequence for a rational number really does just stop, $1/2 = [0;2]$. There's no way to continue the sequence in order to make it infinitely long.

Therefore we can't interleave the continued fractions of two rational numbers whose continued fractions have different lengths. Nor can we interleave the continued fractions of a rational number and an irrational number.

Even if we could make interleaving well defined we would face the problem that continued fractions for rational numbers are not unique. For each rational number there are two continued fractions of finite length that evaluate to give it, one ending in a term $n$ and the other ending in $(n-1) + 1/1$.

$$\cfrac{1}{3+\cfrac{1}{2+\cfrac{1}{4}}} = \cfrac{1}{3+\cfrac{1}{2+\cfrac{1}{3+\cfrac{1}{1}}}}$$

So Cantor's proof failed again.

Cantor's ugly fix

The interleaving map does work as expected for irrational numbers. So Cantor had managed to define a bijection from $\left([0,1)\smallsetminus\mathbb{Q}\right)^2$ to $[0,1)\smallsetminus\mathbb{Q}$.

He finished his proof by separately defining a bijection between $[0,1)$ and $[0,1)\smallsetminus\mathbb{Q}$. To do this he used the fact that that the rationals are countable to define a bijection $\mathbb N\to([0,1)\cap\mathbb{Q})$.

$$0, \frac{1}{2}, \frac{1}{3}, \frac{2}{3},\frac{1}{4}, \frac{3}{4},\dots$$

Let's call this sequence $q$. He also needed some sequence of distinct irrational numbers.

$$\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{3},\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{5},\frac{\sqrt{2}}{6},\frac{\sqrt{2}}{7},\dots$$

Let's call this sequence $r$.

He could then 'make room' for the rational numbers in the style of Hilbert's Hotel, by sending $r_n$ to $r_{2n}$. More explicitly, his bijection was the following.

\begin{gather}h:[0,1)\to\left([0,1)\smallsetminus\mathbb{Q}\right)\\ h(x)= \begin{cases}r_{2n}&\text{if $x=r_n$}\\r_{2n+1}&\text{if $x=q_n$}\\x&\text{otherwise}\end{cases}\end{gather}

Using this map he could then define the bijection he wanted, from $[0,1)^2$ to $[0,1)$, by composing.

$$[0,1)^2\stackrel{h\times h}{\longrightarrow}\left([0,1)\smallsetminus\mathbb{Q}\right)^2 \xrightarrow{\text{interleave}}\left([0,1)\smallsetminus\mathbb{Q}\right)\stackrel{h^{-1}}{\longrightarrow}[0,1)$$

This was the successful version of Cantor's proof that he eventually published. But it had lost some of the simplicity of the elegant 'interleaving' idea.

A better way

Why do neither decimal expansions nor continued fractions provide unique representations? The answer has to do with the order that they use.

Two decimal expansions can be compared by seeing which has the larger digit at the first point at which they differ. We can use this to produce two decimal expansions that are consecutive in this ordering. Pick two consecutive digits, say $3$ and $4$, and then make decimal expansions by following the smaller one with the largest possible digit and the larger one by the smallest possible digit. This produces the expansions $0.3\overline{9}$ and $0.4\overline{0}$. Because of the way we've chosen them there can be no decimal expansion between the two. So they must represent the same real number, because if they represented different numbers $x$ and $y$ then there would be no expansion that could represent $(x+y)/2$.

Similarly, if we look at the ordering on continued fractions we can see that the smallest fraction beginning $[0;3,\dots]$ is $[0;3,1]$, and the largest fraction beginning $[0;4,\dots]$ is $[0;4]$. Again we've produced two representations of the same number, because $1/(3+1/1)=1/4$.

However, this problem with continued fractions only happens because we're allowed to terminate a continued fraction. If all continued fractions had to be infinite then there would be no greatest continued fraction beginning $[0;4,\dots]$, because $[0;4,n,\dots]$ could always be made larger by changing it to $[0;4,n+1,\dots]$.

But if continued fractions aren't allowed to terminate then they can't represent the rational numbers. This is a consequence of the fact that the order on every-other term is reversed. There would be no greatest continued fraction beginning $[0;4,\dots]$, but also no least continued fraction beginning $[0;3,1,\dots]$, and so we would have no way to represent the rational number $1/4$.

This order-reversing property comes from the fact that we used the order-reversing map $x\mapsto 1/x$ in the definition of continued fraction. So to define a nicer representation we simply have to replace this map by an order-preserving one.

Definition 1

Define the function $f$ by

$$f(x)=\frac{x}{1-x}.$$

Then $f$ is an order-preserving bijection $[0,1)\to\mathbb R_{\geq 0}$. The inverse function $g:\mathbb R_{\geq 0}\to[0,1)$ is given by

$$g(x) = \frac{x}{x+1}.$$

Definition 2

Given a real number $x$, we can generate an integer sequence using the same method as the continued fraction, but using $f$ instead of taking the reciprocal. We write $x$ as the sum of its integer and fractional parts, apply $f$ to the fractional part, and repeat the process on the resulting number.

This yields an expression for $x$

$$x=z+g\left(n_0 + g\left(n_1 + g\left(n_2 + g\left(\dots\right)\right)\right)\right)$$

where $z\in\mathbb Z$ is an integer and $n:\mathbb N\to\mathbb N$ is a sequence of natural numbers. We'll notate this representation as

$$\langle z;n_0,n_1,n_2,\dots\rangle$$

where angle brackets have been used in place of the square brackets used in continued fractions.

Note that since $f$ is defined at $0$ we never have to terminate our expression. So every real number corresponds to an infinite sequence. We can now state several nice properties of this representation.

Theorem 3

a) Each real number gets sent to a different sequence.

b) The function from $[0,1)$ to $\mathbb N\to\mathbb N$ given by sending $\langle 0;n_0,n_1,n_2,\dots\rangle$ to $n$ is an order-preserving bijection, where the order on $\mathbb N\to\mathbb N$ is lexicographic (i.e. sequences are compared based on their value at the first position at which they differ).

c) A number is rational if and only if its representation is eventually all $0$s.

d) A number is the root of a quadratic if and only if its representation is eventually periodic.

Each part of this theorem corresponds to similar fact about continued fractions. But generally this representation is simpler. In particular there's no need to worry about nonuniqueness or order-reversal in part (b).

We could prove each part by using the same methods that are used to prove these facts about continued fractions. But it turns out that there's an easier way. Each part of Theorem 3 can be proven easily by using the corresponding fact about continued fractions, and the following Lemma.

Lemma 4

A continued fraction may be converted into the new representation by replacing $n_{2i}$ with $0$ repeated $n_{2i}-1$ times.

$$[z;n_0,n_1,n_2,n_3\dots] = \langle z;\underbrace{0,\dots,0}_{n_0-1\text{ terms}},n_1,\underbrace{0,\dots,0}_{n_2-1\text{ terms}},n_3\dots\rangle$$

The representation of a rational number is obtained by applying the same procedure to the one of its two continued fractions which has an even length, and then appending infinitely many $0$s after the last term.

Proof

We apply the algorithm of Definition 2 to $[z;n_0,n_1,n_2,n_3\dots]$. Its integer part is $z$ and its fractional part is $[0;n_0,n_1,n_2,n_3\dots]$, which can be written as $\frac{1}{[n_0;n_1,n_2,n_3\dots]}$. Applying $f$ to $\frac{1}{[n_0;n_1,n_2,n_3\dots]}$ yields $\frac{1}{[n_0;n_1,n_2,n_3\dots]-1}$, or in other words $\frac{1}{[n_0-1;n_1,n_2,n_3\dots]}$. If $n_0-1 > 0$ then this will have integer part zero, and we must apply $f$ again to get $\frac{1}{[n_0-2;n_1,n_2,n_3\dots]}$. After repeating this $n_0-1$ times we will obtain $\frac{1}{[0;n_1,n_2,n_3\dots]}$, which is equal to $[n_1;n_2,n_3\dots]$. At this point the process repeats.

Some nice proofs

This representation lets us write down a version of Cantor's proof without the fiddly details.

Theorem 5

There exists a bijection $[0,1)^2\to [0,1)$.

Proof

The function

$$(\langle 0;n_0,n_1,n_2\dots\rangle,\langle 0;m_0,m_1,m_2\dots\rangle )\mapsto \langle 0;n_0,m_0,n_1,m_1,n_2,m_2\dots\rangle$$

is such a bijection.

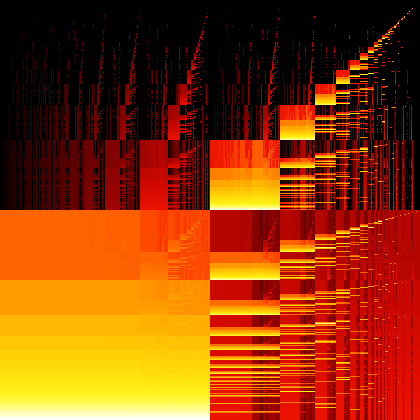
We can visualise this function by plotting it as a heatmap.

(I was hoping that this image was going to turn out to be some mad fractal thing. But in fact it's surprisingly boring. This is because the bijection is actually continuous except at the rational numbers. It's also order-preserving in the sense that if $x\geq x'$ and $y\geq y'$ then $(x,y)$ gets sent to a number at least as large as $(x',y')$.

So I also produced the image you can see at the top of this post, which is what you get if you graph the function $[0,1)^2\to[0,1)$ corresponding to the function $(\mathbb N\to\mathbb N)^2\to(\mathbb N\to\mathbb N)$ which takes two functions $\mathbb N\to\mathbb N$ and composes them. Now that's a mad fractal.)

Finally, we can also present an elegant version of Cantor's other famous result regarding the cardinality of the reals, the diagonal argument.

Theorem 6

There's no surjection from $\mathbb N$ to $\mathbb R$.

Proof

Suppose there was such a surjection. Then by taking fractional parts there would also be a surjection from $\mathbb N$ to $[0,1)$, and by applying our bijection between $[0,1)$ and $\mathbb N\to\mathbb N$ we would obtain a surjection $s:\mathbb N\to(\mathbb N\to\mathbb N)$.

In particular, the map $\mathbb N\to\mathbb N$ given by $n\mapsto s(n)(n)+1$ would be the image under $s$ of some $m\in\mathbb N$. In other words $s(m)(n) = s(n)(n) + 1$ for all $n$. But then setting $n = m$ yields $s(m)(m)=s(m)(m)+1$, a contradiction.

---

Addendum: This post was discussed on Reddit. The Reddit user blobfish1 found an expression in terms of Bessel functions for the real number corresponding to the identity function $\mathbb N\to\mathbb N$.

$$\langle 0;0,1,2,3,\dots\rangle = \frac{J_0(2)}{J_1(2)}$$

Later, I found a paper which defines the same representation, 'Continued fractions and order-preserving homeomorphism' by Francisco Gallego Lupiañez. It contains a nice way of writing the representation.

I wrote it as

$$\langle z;n_0,n_1,n_2,\dots\rangle = z+g\left(n_0 + g\left(n_1 + g\left(n_2 + g\left(\dots\right)\right)\right)\right)$$

where $g$ is the function $x\mapsto\frac{x}{x+1}$. However $g$ can also be written as $x\mapsto\frac{1}{1+\frac{1}{x}}$. Hence we can write a continued fraction where every-other term is $1$.

$$z+\cfrac{1}{1+\cfrac{1}{n_0+\cfrac{1}{1+\cfrac{1}{n_1+\cfrac{1}{1+\cfrac{1}{n_2+\cfrac{1}{1+\cfrac{1}{\ddots}}}}}}}}$$

woodrowconeing.blogspot.com

Source: https://oscarcunningham.com/494/a-better-representation-for-real-numbers/

Share this post